报告人：Lisa Nickerson

整理人：李焕杰

审核人：高家红

2017年9月26日，哈佛医学院/麦克林医院（Harvard Medical School/McLean Hospital）的应用神经影像统计实验室主任Lisa D. Nickerson教授受北京大学麦戈文脑科学研究所高家红老师邀请，在北京大学王克桢楼1113会议室为大家带来了题为：Multivariate and Data-Driven Analysis Methods for FMRI的学术报告。Nickerson教授的主要研究方向为脑功能磁共振成像数据多参数统计模型和多模态磁共振成像数据融合分析，及其在药物成瘾方面的应用。在本场讲座中，Nickerson教授着重介绍了基于多参数的脑功能磁共振成像数据分析方法（独立成分分析，ICA）和基于数据驱动的双重回归（dual regression）方法，及这两种方法在静息态和任务态脑功能磁共振成像数据上的应用。

概 述

脑功能磁共振成像技术自二十世纪九十年代问世以来，凭借安全、无辐射，较高时空分辨率等优点，正日益成为探索和认知大脑功能奥秘的首选工具。如何基于脑功能磁共振成像数据挖掘出准确可靠的大脑信息是目前神经影像学家认识大脑的主要途径。传统的标准任务态脑功能磁共振成像数据分析方法主要基于一般线性模型（general linear model）,认为每个体素的时间波动是由多种变量引起的线性加权之和决定的。然而一般线性模型认为每个体素的时间波动是独立的，忽略了相邻体素间和相同脑功能区的时间波动相关性影响。同时头动、机器噪声等伪影也会对一般线性模型产生影响，导致统计结果的偏差。另一方面，静息态脑功能磁共振成像数据（rfMRI）为大脑自发活动信号，可用于脑功能网络的分区。典型的基于rfMRI数据的脑功能网络检测方法为种子点方法（seed-based RSFC）。在该方法中，所有与选定种子点高度相关的体素被认定为同一脑网络。然而在同一脑区选不同的种子点，会得到不同空间结构的脑网络，这是由于选定的种子点不只属于同一个脑网络。综上，无论是分析任务态fMRI数据的GLM模型，还是分析rfMRI数据的种子点方法都是单参数（univariate）方法，即每次只分析一个体素。Nickerson教授在这个报道中为我们介绍了目前国际上越来越受重视的多参数（multivariate）方法来分析fMRI数据，多参数方法不同于单参数方法，可同时对多个体素进行分析。在这次报告中，Nickerson教授介绍的用于分析fMRI数据的主要多参数方法为独立成分分析(ICA)和双重回归分析（dual regression）。

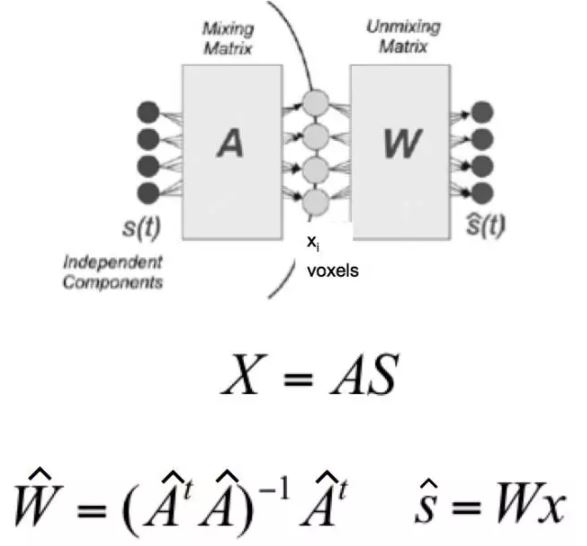
图1. ICA原理示意图

研究方法：ICA

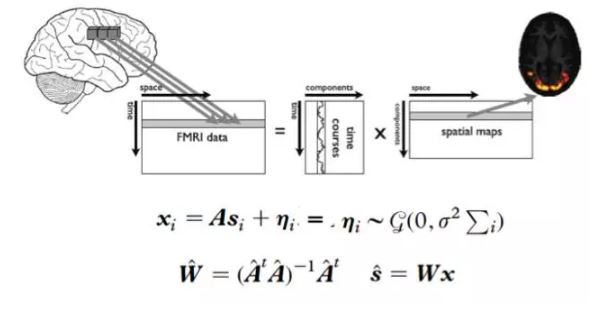
ICA又称盲源分离(Blind source separation, BSS)，它假设观察到的随机信号X服从模型X=AS，其中S为未知源信号，其分量相互独立，A为一未知混合矩阵。ICA的目的是通过且仅通过观察x来估计混合矩阵A以及源信号S。基于个体fMRI数据的ICA分析如图2所示，可基于特定的时间序列得到相应的被试特定（subject-specific）空间图像，也可根据给定的空间图像得到相应的被试特定的时间序列。

图2. 个人fMRI数据ICA分析

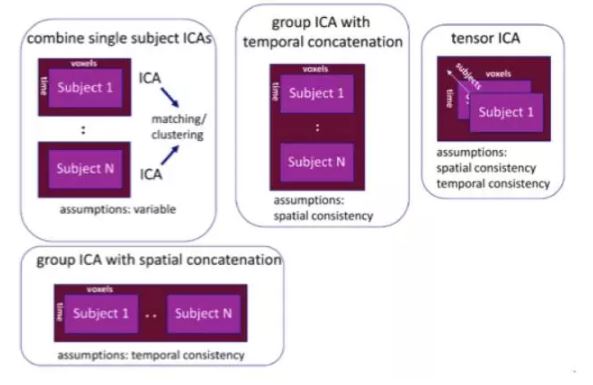
Nickerson教授着重介绍了组间ICA分析，如图3所示。其中group ICA with temporal concatenation 是最常用的组间ICA分析方法，该方法假设所有被试对应同一时间序列有相同的空间图像，由于大脑的脑网络分布几乎是一致的，因此该方法适用于对rfMRI数据进行脑网络的分割分析，得到组间脑网络。另外，Tensor ICA也常用于组间fMRI数据分析，该方法假设组间数据在同一体素间有相同的时间序列，因此适用于分析任务态fMRI数据。Nickerson教授指出组间ICA除了确定组间脑网络和组间时间序列外，还可以用于得到个体间的被试特异性的脑网络图（subject-specific spatial maps, SSSM）和脑网络对应的时间序列(Subject-specific timecourses, SSTC)，用以研究组间脑网络差异。

图3. 组间fMRI数据ICA分析

研究方法：Dual regression

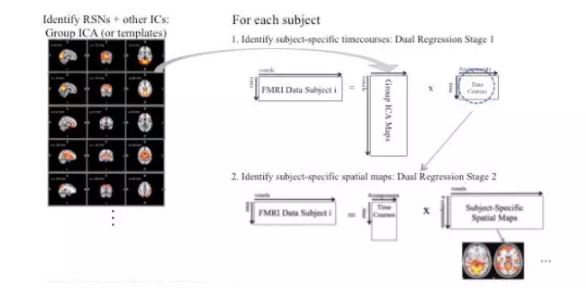
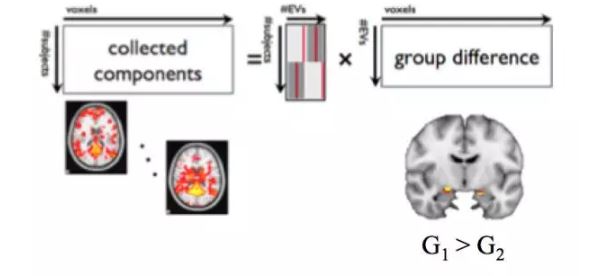
Dual regression可在基于组间ICA得到组间脑功能网络的前提下，得到相应组间脑网络的SSSM和SSTC，具体流程如图4所示。Dual regression对每个被试的4D fMRI数据进行分别分析，首先基于组间ICA得到的空间脑网络图，得到对应不同脑功能网络的SSTC，然后利用不同脑网络的SSTC得到组间脑网络对应的SSSM。选出感兴趣的脑功能网络，将基于dual regression分析得到的所有被试的该脑功能网络对应的SSSM合成4D数据，进行组间分析，如图5所示。组间差异可以反映出脑网络空间形状的差异或脑网络振幅的差异。Nickerson教授特意指出在进行dual regression分析时，为保证组间结果的准确性，要对所有网络的SSTC分别进行标准化得到标准偏差为1的SSTC。

图4. Dual regression示意图

图5. 基于Dual regression的组间脑网络差异分析

综上，多参数dual regression分析能够用于区分单独脑网络的连接情况，包括脑网络空间形状和脑网络振幅。

Nickerson教授也用组间ICA和dual regression研究任务态fMRI数据，确定任务状态下的脑网络。实验数据来自于Human Connectome Project, 共收集10793个任务态的COPE图像，分别来自于7个不同的fMRI实验任务 。具体流程如图6所示，将所有被试的不同任务下的4D COPE图像合成一个4D数据，进行多参数回归分析，以20个组间脑网络图像为模板，得到不同脑网络对应的不同任务下的被试间响应（subject-courses）。为评价不同任务下的脑功能网络和脑网络活动强度与任务执行程度的关系，用GLM 模型对不同任务得到的subject-courses和相应任务的评价标准做线性相关分析。

图6. 组间任务态fMRI数据分析

总结，基于上述rfMRI和任务态fMRI的研究，Nickerson教授指出单参数分析：GLM模型或种子点功能连接方法，得到的是一个集合的脑网络，不易于区别为特定的（更精细）网络，这样得到的脑网络会混有由噪声引起的脑网络。多参数回归方法能够区分出任务态或静息态fMRI图像的不同脑功能网络，找出与任务相关的特定脑网络，避免运动或其他噪声带来的影响。同时多参数回归方法能够用于评同一脑网络内或不同脑网络间的连接情况、脑图像形状或振幅差异；评价特定网络在特定任务下的激活情况等。

在本次报告中，Nickerson教授为大家详细地讲授了多参数回归方法的基本原理和在fMRI数据中的应用实例，让大家受益匪浅。

参考文献

1.Nickerson, L.D., Smith, S.M., Öngür, D.,Beckmann, C.F. 2017. Using Dual Regression to Investigate Network Shape andAmplitude in Functional Connectivity Analyses.Front Neurosci.11:115

2.Beckmann, C.F., Smith, S.M., 2004.Probabilistic Independent Component Analysis for Functional Magnetic ResonanceImaging. IEEE Transactions on Medical Imaging. 23(2):137-152.

3.Beckmann, C.F., 2012. Modelling with independent components. NeuroImage. 62:891-901.