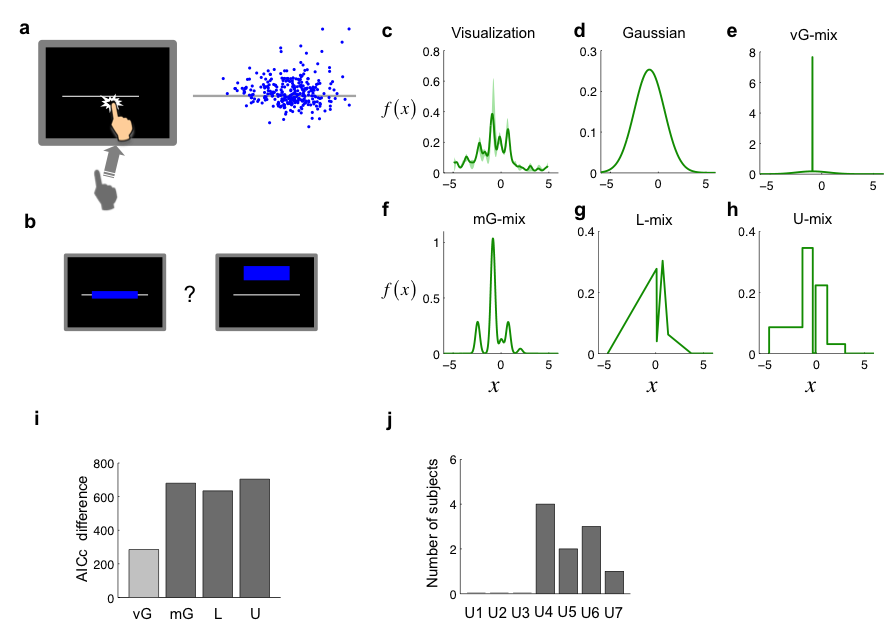
Figure 5. Experiment 2. (a) The reaching task. Left: The task. Same as Experiment 1 except that a horizontal line was used as the target. Right: The endpoints for one subject. (b) The choice task. Similar to Experiment 1 but each pair of targets consisted of a rectangle on the line and a rectangle off the line. (c) Non-parametric visualization of the internal pdf for one subject. Shaded regions denote ±SEM. is in the unit of the subject’s vertical standard deviation estimated from the reaching task. (d–h) Internal pdfs estimated from different models for the same subject. (i) AICc difference between the Gaussian model and the other four models summed over the 10 subjects. The unimodal models (including vG-mix) and mixture models are respectively coded in light gray and dark gray. Positive difference indicates better fit. (j) Number of subjects best fit by each U-mix model. 

在许多运动决策的实验任务中，被试会补偿自己的运动误差，其绩效趋近于最大化可能的奖赏。这意味着被试能够将误差分布的信息与不同运动结果对应的价值整合起来。要找到最优决策，人脑必须了解各种不同运动的误差分布的概率密度函数，并对此进行复杂的运算。而人脑如何表征这样的概率密度函数以及如何实现相关运算尚属未知。在三个实验中，我们采用了一种新颖的行为任务和建模方法来测量人脑如何表征快速指向运动中的随机误差。在每个实验试次中，我们要求人类被试判断两个目标中的哪一个自己更容易击中。通过比较被试在不同形状和大小的目标下的决策行为，我们可以构建出被试对其运动误差随机分布的内部表征。我们也测量了每个被试实际的运动误差。虽然被试实际运动误差的随机分布是单峰的、接近于高斯分布，被试的内在表征却常常是多峰的，近似于对少量基本正交的（即，不重合的）基底分布的线性加和。相比高斯混合分布等其他的混合分布，以均匀分布为底的混合分布能够更好地解释被试的运动决策。

Zhang H*, Daw ND, Maloney LT. (2015). Human representation of visuo-motor uncertainty as mixtures of orthogonal basis distributions.  Nature Neuroscience . DOI: 10.1038/nn.4055